Two Whys Behind Positional Encoding in Transformers

Posted May 19, 2025

By sri-dhurkesh

5 min read

First Why:

Why do we need positional encoding in word embeddings instead of passing the embedding vectors directly to the attention mechanism?

Second Why:

Why do we use sinusoidal functions for positional encoding instead of other functions or methods?

First Why – The Need for Positional Encoding

The embedding vector alone lacks information about the position of words in a sequence, while the attention mechanism is permutation invariant.
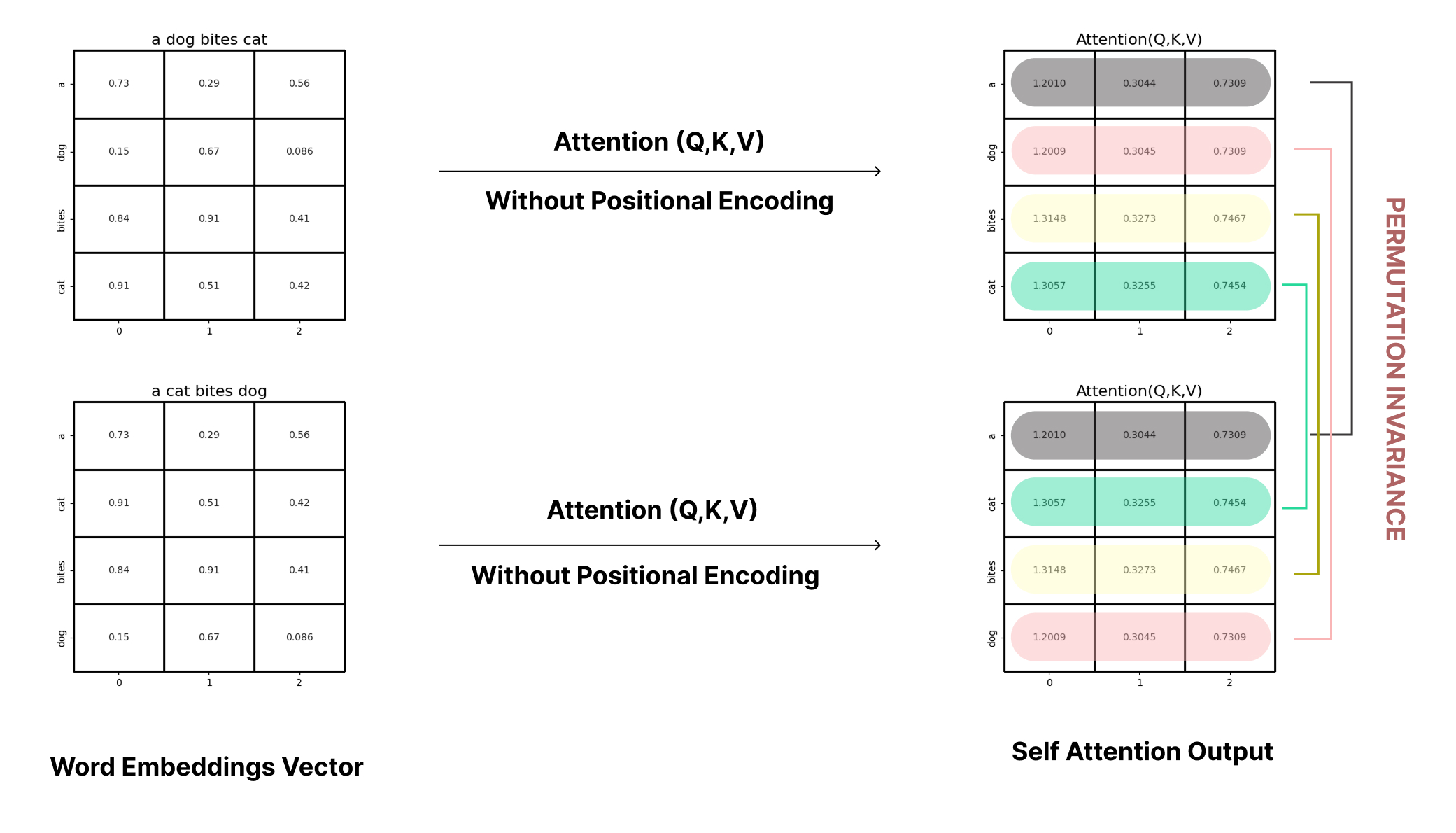
Permutation invariance means the output of the function does not change even if the order of inputs is altered, i.e., F(a, b, c) == F(b, c, a)
To explain permutation invariance (Ref: Fig-1):
- Consider two sentences: "a dog bites cat" and "a cat bites dog".
- After vectorizing and embedding them into a 4×3 matrix (4 tokens, 3-dimensional embeddings), calculate the attention matrix without positional encoding.
- You’ll notice that the word "dog" gets the same vector [1.2009, 0.3045, 0.7039] in both sentences, despite having a different meaning due to word order.
- This happens because the attention mechanism treats the input as a bag of words—it lacks any sense of sequence.
- In tasks like translation, this lack of positional understanding leads to semantic errors.
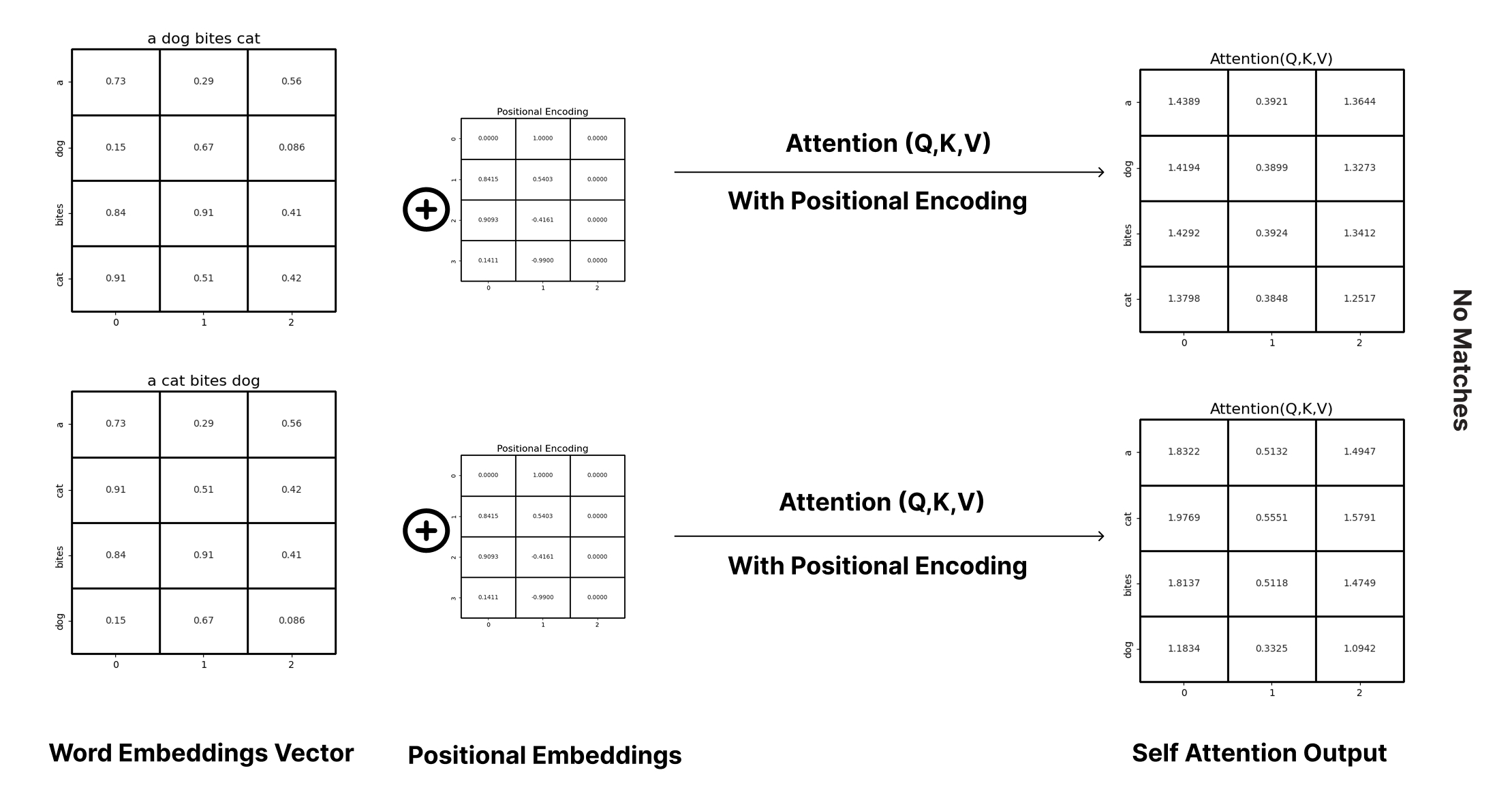
- To address this, positional encoding is introduced (Ref: Fig-2).
- As shown in Fig-2, adding positional encoding to the embedding vector incorporates position-dependent information.
- Now, calculating the attention matrix produces different vectors for the same word in different positions, capturing the sequence semantics more effectively.

Fig 1: Self attention matrix without positional encoding

Fig 2: Self attention matrix with positional encoding

Second, why - Need for the Sinusoidal Function:

One might consider using the token index directly for position information. However:
- Indices are unbounded, non-differentiable, and provide no structure for learning relative position.
- Sinusoidal functions, on the other hand, are:
  - Bounded: Range between -1 and 1.
  - Smooth and differentiable: Favorable for gradient-based learning.
  - Periodic: Encodes position cyclically, allowing the model to generalize to longer sequences.
A challenge with periodicity is the repetition of values. To mitigate this, multiple dimensions are assigned sinusoidal functions of varying frequencies.
By using a range of frequencies across dimensions, we generate unique and informative encodings for each position, enabling the model to capture both absolute and relative positional relationships effectively.

Figure-3

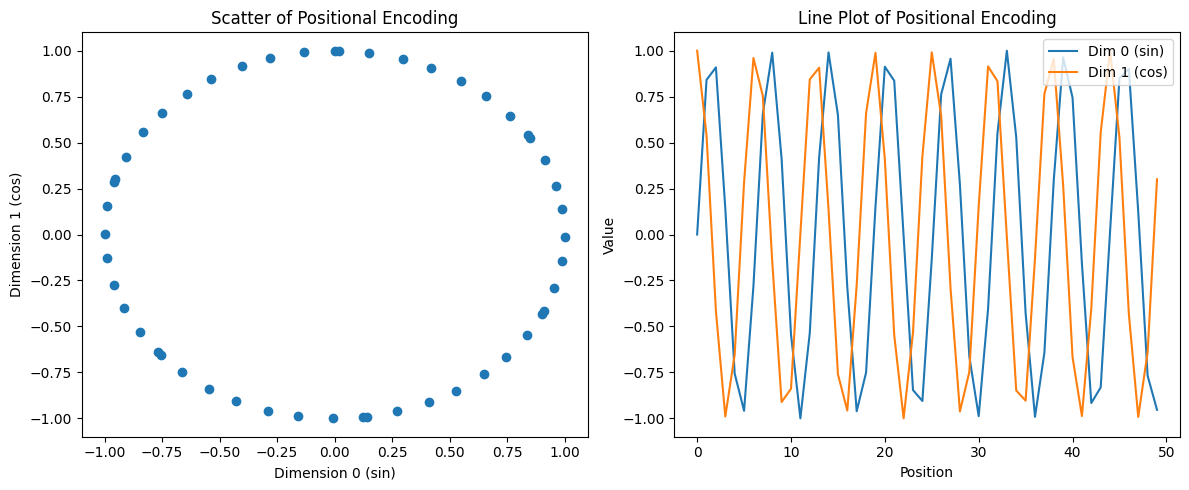
To visually understand how sinusoidal positional encoding captures relative positions, let’s consider a simplified 2D example for a sentence containing n tokens. In this setup, positional encodings are computed using sine and cosine functions. If you plot these values with sin(position) on the x-axis and cos(position) on the y-axis, as shown on the left side of Figure 3, you get a circular pattern. This is expected, as points defined by sine and cosine of an angle naturally trace a unit circle.

The plotted data in Figure 3 is generated using the following code:

  
data = getPositionEncoding(total_tokens=10, d=2)
print(data)

# Output:
array([[ 0.        ,  1.        ],
       [ 0.84147098,  0.54030231],
       [ 0.90929743, -0.41614684],
       [ 0.14112001, -0.9899925 ],
       [-0.7568025 , -0.65364362],
       [-0.95892427,  0.28366219],
       [-0.2794155 ,  0.96017029],
       [ 0.6569866 ,  0.75390225],
       [ 0.98935825, -0.14550003],
       [ 0.41211849, -0.91113026]])

This circular representation is not arbitrary—it visually demonstrates the rotational symmetry of sinusoidal functions. Since rotation preserves angles and relative positions, any position on this circle can be transformed into another via rotation. This is the key insight that allows Transformer models to capture relative position using linear transformations.
On the right side of Figure 3, sine and cosine values are plotted separately against token positions. These periodic waveforms vary smoothly and encode both absolute and relative position information in a structured manner.
However, sine and cosine are periodic functions and would eventually repeat. To avoid ambiguity and allow more expressive encodings, the Transformer uses multiple dimensions (frequencies), each capturing different positional patterns. This ensures unique and distinguishable encodings even for longer sequences.
To understand how relative positions can be derived, consider the rotation matrix transformation property:
\[\begin{bmatrix} x' \\ y' \end{bmatrix} = R(\theta) \cdot \begin{bmatrix} x \\ y \end{bmatrix} \quad \text{where} \quad R(\theta)=\begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}\]
- This matrix allows us to rotate a position vector by an angle $\theta$ When applied to the 2D sinusoidal encoding $[\sin(w_i \cdot p), \cos(w_i \cdot p)]$, we can transform it to a new position:

\[\begin{bmatrix} \sin(w_{(i)}(p+k) \\ \cos(w_{(i)}(p+k)) \end{bmatrix} = M_k . \begin{bmatrix} \sin(w_{(i)}) \\ \cos(w_{(i)}) \end{bmatrix}\quad Where,\quad M_k = \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix}, w_{(i)} = \frac{1}{10000^{\frac{2i}{d}}}\]

Note: In NumPy, the x and y axes are switched compared to the standard mathematical convention. This means that a rotation through angle θ with non-standard axes results in the matrix $M_k$ being represented by $R(\theta)^T$ (the transpose of the rotation matrix).

Here, $M_{k}$ acts as a transformation matrix that rotates the original encoding to reflect a relative shift or offset $k$ representing calcualting the relative position from $p$ to $p +k$ Since sine and cosine form an orthonormal basis, this transformation preserves structure and enables relative position calculation.
This approach is highlighted in the original Transformer paper ”Attention is All You Need“:

“ We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset $k$, $PE_{pos+k}$ can be represented as a linear function of $PE_{pos}$.”

Thus, using sinusoidal positional encodings, we can compute any relative position from any given position through simple transformations. For instance, if you’re at position 2, you can derive the positional encodings for positions 1, 3, 4, 5, etc., using this rotational property.

In summary:

The unit-circle representation (left plot) reflects the rotational symmetry of the encoding.
The periodic waveform representation (right plot) reflects the encoding of absolute position.
By increasing dimensionality with multiple frequencies, positional encoding avoids ambiguity.
Most importantly, through rotation matrix transformations, we can derive relative positions efficiently and mathematically, making sinusoidal encoding highly suitable for attention mechanisms